

最近幾年以來,在音頻放大器中用上大量的負回授已然成為爭論的焦點所在,因為有些人在測試過回授放大器的時間響應(time-response)特性後,曾獲致下述結論:放大器採用大量負回授的設計後,很容易引起一種高頻失真,那就是暫態互調失真(Transient Intermodulation Distortion, TIM);簡單的說,就是在信號變化太快使得放大器「跟不上」的時候,就產生這類失真了。
而這種大量負回授會引起TIM的結論,似乎和有關負回授的傳統觀念互為逕庭;蓋我們一直都認為在維持相當程度穩定性的前提下,增加負回授能改進放大器的特性。所以,最近又有一派人仕對前面所提到的立論提出質疑,而他們的結論是:大量負回授不會嚴重增加TIM,同時只要放大器有相當程度的轉折率(Slew Rate),事實上反而會對放大器的特性有所助益。
TIM就這樣成為一個相當時髦的主題,環繞的是一些「公說公有理,婆說婆有理」的爭論,同時TIM也成為音響不好的眾矢之的。這種情形我們也可以從一些音響廣告看出來,有些廠家也受到這種立論的影響,因為這些廣告曾沾沾自得的大肆宣傳他們的產品「負回授用得極少」。
似乎有關此一主題的誤解和爭論泰半是由於我們對應用負回授後所引起的利害各半和限制想法不愓之故,這特別是在提到目前實際生產的線路時為然,尤其對回授所做補償的一部份更為如此。是以本文在必要時也會花一點時間回顧一些重要的負回授原理,如能測底了解施加在音頻放大器中的負回授真實特性,有助於解決一些有關TIM的問題。
在進入正題以前,要指出一點,即與負回授及其補償有關聯的TIM,只是高頻互調失真的一種,由於我們一向慣於用「動態互調失真」(Dynamic Intermodulation Distortion, DIM)來表示不僅和振幅而且和頻率有關的互調失真,因此TIM是DIM的一種。而頻率和振幅的乘積正意味著「變率」(ra-te-change),同時放大器能「跟得上」的最大變率值就是轉折率,因此「轉折誘致失真」(Slew Induced Distortion, SID)也可以用來表示DIM。然而,這種區分由於涉及失真產生機構的成分大於能測得或聽出來的影響,而顯得相當薄弱和無關宏旨。只因為這是大多數爭論的起源,我們的重點就放在TIM上,但是往後我們的討論也會提及其他引起的TIM來源,因為其中有些的影響實際上更為嚴重。
暫態互調失真
首先,我們要看一看這些有關TIM的爭論,以期了解其背景,以下就是綜合改寫自各家之言的一段。
回授放大器的工作原理是:輸入信號的大部分為取自放大器輸出的回授所抵消,只由少量的「信號加上誤差」來推動放大器,以獲得所預期的輸出。因而在有大量負回授的放大器裡,這種「信號加上誤差」被限制得很低,是以在理論上所生失真也少。在這種情形下,計入回授效果的增益淨值(閉迴路增益)幾乎完全視輸出信號回授的多寡而定,如果說回授量為十分之一,增益就是10,因此大回授因數(feedback factor,沒有回授的增益和計入回授的增益之比值)之獲致,是由於讓開迴路放大器的增益加大之結果,因而這個開迴路(open-loop)的放大器相當敏感,同時在誤差因某原因變得全然可以感知時,就會過載。
放大器的輸入和輸出間的遲延(dalay)有限,如果推動回授放大器的信號上升時間相當快(如方波的前緣),則輸入信號要完全進入開迴路放大器就得要有一段時間了,同時又不會因尚未回到輸入端的負回授而減少,因而會過載,失真也就發生,回授因數高的放大器輸入愈敏感,愈容易導致此類過載。
由於這種失真是輸入信號的快速暫態所引起的,又因為過載會導致互調失真,所以這種現象稱之為暫態互調失真,簡稱TIM。
現在再回到TIM的肇因上去,由於對開迴路放大器所做必要的回受補償會使響應更加遲緩,使得情況更加惡化,而多級放大電路中的每一級都會產生隨頻率上升而增加的相移(phase shift),但是由於回受補償會使開迴路響應滑落(roll off),因而使得在這些相移累積到足以導致不穩定或閉迴路響應到達峯值以前,回授因數降至1時的頻率就是增益交越頻率(gain crossover frequency),為了要獲致穩定的增益交越頻率,這種因每個八度音程(octave)作6dB補償所造成的滑落必須在較低的頻率就及早開始,而低頻時回授因數大的放大器,由於必須「清除」的增益較多,更要在較低的頻率就開始補償滑落,這因而使得開回路頻寬變得較小。試想一個回授量20dB的放大器,若其增益交越定在1MHz,則在100KHz以前尚無需滑落,然而回授量若為60dB,在1KHz就得開始滑落了,後者由於回授補償程度較重,同時其開迴路時間常數也較長,故而對輸入信號的響應較慢。
為了及時響應快速的輸入信號(例如說:方波),必須要有一個夠大的內部電壓或電流超越量(overshoot)來使補償電容快速充電,並克服因之而起的長時間常數所造成的影響。而當一個大的誤差信號加在這個開迴路放大器上時,所需的超越量是在快速的輸入變化及回授「追上」輸入所需時間的區間內產生的。
在某些情形下,這種超越量可能是該點信號電平的10至100倍;不幸的是,在補償點之前的放大級通常無法從容的處理這麼大的信號,必然會有非線性或全面割切產生。如果這個超越量真的使這些放大級產生割切現象或產生失真,TIM就發生了,當超越量遭到割切後,放大器就進入我們所熟知的轉折率限制下了。
如果輸入信號的頻帶能限制在低於放大器的開迴路頻寬範圍內,我們就可以用數學來證明不會有超越量產生,即令輸入信號是一個頻帶受限制的方波也一樣。因此,寬一點的開迴路頻寬能消除由超越量引起TIM的可能性。其次,擁有寬一點的開迴路頻寬,能限制已定增益交越頻率下的回授因數;例如說,如果我們選定的開迴路頻寬是20KHz,而增益交越頻率為1MHz,則回授因數就限制在34dB了。
上述有關TIM的說明似乎是蠻有道理的,也以不同面目出現在許多場合,這也是時下盛行的觀念的出發點,即小回授因數及寬開迴路頻寬是減少TIM所必須的。乍看之下這種立論很有說服力,而事實上,這種說法有些過於簡單及易於引起誤解,儘管說某些問題曾在許多技術性論文上分析過,但卻忽略其他更重要的研究,在某些方面可以說是犯了「見樹不見林」的毛病。
此處我們要研究的是一些更廣泛、更深入的問題,譬如說,我們要研究一下到底一般音響節目的信號有多快,而放大器中不可避免的時間遲延有多長;至於如何受到回授補償的影響,則是另一個值得深入研究的重要領域。同時我們還要測定支配放大器內部各級過載的條件,這些研究都將藉一個綜合了回授因數及開迴路頻寬在內的實際放大線路來完成,同時在認知了除開振幅外,放大器也受限於要在輸出提供一個最大的變率以後,我們也會對放大器的轉折率特性及其和TIM的關係多加注意,最後還會提到測試放大器TIM特性的技術。
節目特性
節目源和所有的放大器一樣,頻帶都是有限制的,沒有任何一個節目源能產生有刀片般鋒利邊緣的方波。事實上,節目源不僅在小信號方面的頻帶有限制,其在大信號頻寬或功率頻寬上受有更嚴重的限制。舉例來說,一部優良的磁帶錄音機,低電平時或許在20KHz處仍能維持平直的特性,但一定無法在20KHz產生滿額的輸出,這種限制通常是由於等化過程中,先將高頻預行強調(pre-emphasize),以期在重播時的解強調(de-emphasis)能減少高頻雜音,因而高頻較低頻更易於讓錄存媒體過載,這種等化過程對幾乎所有的節目源都一樣,包括唱片、調頻廣播及磁帶在內,結果是每一個節目源的最大高頻輸出都受限於一個相當程度內。
由於變率或「時間導數」(time derivate)大的信號一般說來是TIM的肇因,我們要找出一個方法來顯示出已定節目源產生TIM趨勢的特性,這種方法必須和時間導數一樣,不能是絕對的,而要是相對的,才能同等適用在系統上不同的點,而不需考慮信號的電平如何。因此我們採用峯值時間導數和峯值振幅的比值來表示,其單位為「每伏特每微秒的伏特數(V/μS)/V,並稱之為常態化(normalized)的時間導數,這個數值的導數和大信號的上升時間相似,但並不十分相似,認識了這個常態化時間導數後,我們就可以在系統中通行無阻了,蓋有了系統中某一點的最大振幅後,就可以決定相對的最大時間導數。
除了麥克風外,家庭中最好的快速節目信號源可能是唱片,然而其特性受到循軌(tracking)之類機械過程的限制極多,是以其性質相當有特性的,在圖一中的點狀分佈曲線,是測試許多唱片在各種頻率時由觀察所得的最大輸出電平,而這些數據是取材自Shure公司廣泛發行的循軌能力圖。其一般表示法都是以音槽速度(groove velocity)來表示的,這個信號業已經過RIAA等化,並加以常態化定在1KHz即1V峯值時為25cm/S,而所示者為唱頭等化放大器的輸出,(這個數據對RIAA等化以前的系統各點是無效的,例如說唱頭等化放大器的輸入端便是如此),而「X」狀的數據則是單響鐃鈸聲的頻譜數據,這一聲鐃鈸聲則是取材自Sheffield實驗室出品的直接刻錄唱片,素以循軌困難出名。
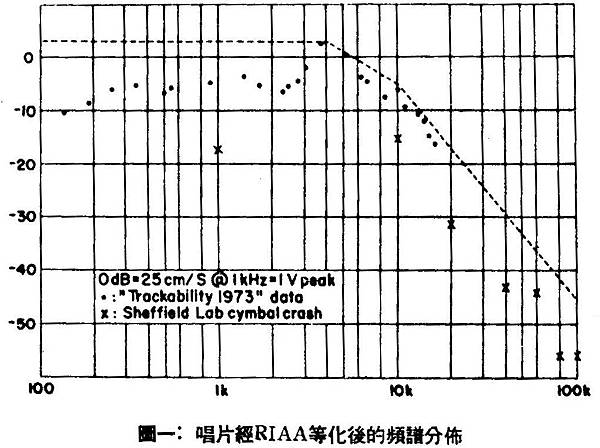

由圖一我們可以看出,最大振幅發生於4KHz處,其峯值為1.35V,而最大時間導數發生於10KHz處其值為0.035V/μS,使得常態化的時間導數只有0.026(V/μS)/V。因此,在一個會遭遇到如圖一中點狀分佈所示的廣泛訊源的系統裡,若要能低失真的處理一個峯值為1V的振幅,就必須要能同樣低失真的處理一個0.026V/μS的時間導數。
在進入更深的討論前,有一件事要注意到,那就是高級的高音控制電路有增加節目源常態化時間導數的傾向,但程度不會像第一次想到這一點時所感受般嚴重。我們可以對圖一詳加檢視而獲得其理由,峯值時間導數會隨高頻信號振幅加大而等比例增加,而大多數的高音控制是在2KHz及10KHz間工作,因而意味著全面的峯值振幅(圖一中的4至5KHz之間)也會有些許增加,基於這些觀察,我們可以獲致下述結論:每6dB的高音提升會使常態化的時間導數增加約50%。
而鐃鈸之一擊含有大量的超聲波成分,其振幅通常低於其他點所形成的包覆線,要注意實際上中頻的錄製電平比較起來是相當低的。因此,單獨看起來鐃鈸聲的常態化時間導數相當高,但我們的重點是放在所有音樂的峯值振幅上的。
即使我們忽略掉圖一的三個最高點,也能有低於10KHz的全面功率頻寬,使得最大常態化時間導數約為0.05(V/μS/V,由比較可得20KHz正弦波的常態化時間導數則是0.126(V/μS)/V。
音樂中自然會有許多同時存在的點,其振幅和時間導數能以某種方式相加,得以產生一個完全頻譜的整體振幅和整體時間導數,瞭解到在500Hz及2KHz之間的中頻頻率時,經RIAA等化後的振幅和錄製速度直接有關以後,就可以得到進一步的認識。至於2KHz以上的信號,RIAA等化後的時間導數和錄製速度有直接關聯,及50cm/S、10KHz的成分在唱頭等化放大級輸出所生的時間導數和20cm/S、20KHz所生相同,這種關係是由於2KHz處RIAA高頻滑落的積分效果。瞭解到這一點以後,我們就能找出一個好辦法來決定常態化時間導數,即最大的整體中頻速度即最大的整體高頻速度實值可藉假設而得,要記住最大中頻速度的假設值較小時,就會有較大的常態化時間導數,同時要注意中頻和高頻的最大值未必要同時發生。
比如說,如果我們假設最大中頻速度是25cm/S,而又把最大高頻速度假設得大一點,假設為150cm/S(大概無法循軌了),我們所得到的數字是0.076(V/μS)/V,由這個數字我們可以得知,一個能在8歐姆負載上產生40V峯值的100瓦放大器,必須能夠清楚的再生時間導數為3V/μS的信號。
這個數值對某些人來說可能會認為很小,但關鍵在於「清楚」這兩個字上。誠然此處我們尚未談及放大器的轉折能立極限,這通常是在非線性的工作情況下發生的,但很明顯的是為了要滿足「清楚」的要求,放大器必須要有一些工作邊際,稍後我們會看到,在某些情況下,這個轉折邊際的要求相當大。
雖然說,極不可能有任何節目源會有0.076(V/μS)/V的數值,但我們可以更保守些,我們可以要求整個系統能再適當的轉折邊際要求下處理一個滿幅的20KHz正弦波,即0.125(V/μS)/V。如果還要進一步的要求能「清楚」的處理一個頻帶受限於20KHz、0.25(V/μS)/V的方波,則是把保守傾向中的另一個因素也加入了。
基於這些觀察,我們可獲致下述結論:實際的音響信號並不像某些人所深信般的快速,然而我們不可因而自滿,因為這種認識只是讓我們能更深入實際的應付TIM的問題。
低通濾波器
經常有人主張,為了將TIM減少到最低的程度,應當在功率放大器前面加上一級低通濾波器(low-pass filter, LPF),來確保節目的頻寬不致超過放大器的開迴路頻寬。儘管稍後我們會看到這種預防措施和TIM的感受程度沒有關聯,但值得注意的是LPF會限制住功率放大器輸入信號的功率頻寬,時間導數也因而受限。在這方面,如果這種限制有必要的話,這個LPF就能防止TIM。然而,先前我們的討論曾指出,實際音響信號的功率頻寬比20KHz小得很多,是以設若由於頻率響應的誤差(在20KHz處假設有一階截止時為-1dB),使得低於40KHz時LPF未必會截止(Cutoff),我們就可以安心的說這種濾波電路對節目信號所引起的TIM沒有影響。
然而滴答聲(ticks)、劈啪聲(Pops)即循軌不良等所生的常態化時間導數卻比正常節目源所生者大或可能出現高達0.1或0.2(V/μS)/V的數值。然而,就算是步級式(step)的輸入,40KHz的LPF也只能限制到0.25(V/μS)/V而已。是以這種濾波器對常態化時間導數值較小的滴答聲、劈啪聲及循軌不良等現象的效果有限,同時人們必然也會感到好奇,何以對這些惱人的信號對吳TIM的再生是如此重要?或許該這麼說明才夠充分:如能達成這個目的,這個系統就不致有轉折率的限制了。
回授補償
前面曾經提過,回授的工作原理再於把輸出的一部份送回輸入來,和輸入信號加以比較,而行程的迴路如果信號的相位不正確的話就會產生不穩的狀態。回授補償就是藉著對淨增益和信號行經此一閉迴路時所生相移的控制來確保穩定性。
由於回授補償所扮演的角色已瀕臨於TIM失真的產生機構,又由於許多有關TIM的討論曾對回授補償做過不當的批判,故而在這個時候來看一看回授補償是再恰當不過了。
由於所有放大器的頻寬都是有極限的,是以在某個頻率時,增益乃至回授因數必然開始滑落,在多級(multistages)放大器裡,通常每一級都有一個或數個極點(pole)(每八度音程6dB的滑落),同時也有相移產生。如果在某一高頻時相移太大,而迴路中仍有增益存在,就變成正回授,因而形成振盪電路了。因此回授因數降為1的頻率(即增益交越頻率)。在決定放大器的穩定性時極為重要;為了防止振盪,在固定為180°的倒相迴路中,該頻率的相移累積必須少於180°。一般說來,良好的工程經驗會要求相移累積必須少於135°,以期留有至少45°的相位邊際,同時為了獲致預期的穩定性,可用回授補償來使增益從容的滑落,以期在相移累積太大時能讓回授因數降到1以下。


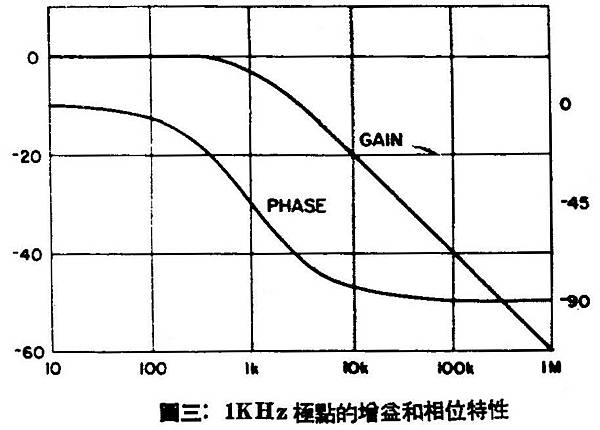
圖二所示為典型的功率放大器在運用回授補償以前及之後的開迴路增益,用頻率的函數表示,而閉迴路增益則是26dB處的虛線所示,回授因數就是實線和虛線間的距離。有一點很重要必須要記住,每一次的滑落均導致相移(相位置後或延遲),同時這種相移是隨頻率而增加的,但決不至超過90°,在3dB點或角頻率(corner frequency)處,每次滑落所生相移為45°。單極點系統的增益即相位特性如圖三所示,要注意單極點位於低頻時,雖不會引入超過90°的相移,卻會產生大量的高頻損失,這就是滯後補償的基礎。

在增益交越頻率之下有多個極點的設計會有不穩的傾向,如果只有單極點的話,確有穩定的趨勢,即令此一極點是位於極低的頻率。圖二中未經補償的放大器其交越點在2.4MHz之下有三個極點,而補償過的放大器在1MHz處交越,只有一個即點位於增益交越頻率之下;如圖二所示的情形,補償網路通常會大幅的降低一個既存極點的頻率,同時也會顯著的增加另一個極點的頻率,這種效果叫做極點分割(pole splitting),其雙重效益更進一步的加強了穩定性。
總而言之,回授補償的目的相當簡單:即建立一個相當低的增益交越頻率,來獲致合乎要求的相位邊際,在功率放大器中,多數的高頻相移是由輸出晶體所造成,其典型的ft(電流的增益──頻寬乘積)約為1至4MHz,超過此頻率,輸出及的相移有多快速增加的傾向;因此,功率放大器合理的增益交越頻率一般說來是在0.5到2MHz之間。
典型的功率放大器實例
為求進一步的了解,我們現在要簡要的回顧一下實際功率放大器的工作情形。


圖四所示是一個相當流行的放大器電路的簡化圖,這個電路也會在稍後用來做有關TIM討論時的圖例。電晶體Q1及Q2形成差動放大電路,是這個開迴路放大器的第一級,加在Q2基極的回授信號自Q1基極的輸入信號中減去,要注意回授信號為R4及R3分壓,而使閉迴路增益設定在20左右,電容C2能隔絕全部直流回授,以維持少量的輸出中點(offset)電壓。
在Q1及Q2基極間的電壓差可演繹成一個電流信號,依次推動Q3的基極電路,而Q3集極上的電壓信號為「幾近單位增益(unity gain)的互補型達靈頓射極隨耦輸出級」輸出,輸出級的主要目的就是要提供電流增益,因而成為Q3集極電路上阻抗相當高的負載。而Q3的集極電流是由一個電流源所供應,是以Q3集極的唯一實際負載就是輸出級所呈現的阻抗,這種配置在預行推動級(prerdriver)Q3提供極高的增益,特別是當輸出級的電流增益很高時。
此一放大器未經補償的迴路增益如圖二的上層曲線所示(假設電晶體的β值為50),而其回授補償的工作只由一個電容器C3來擔任,連接在Q3的集極和基極間,這種方式的補償通常稱做密勒效應(Miller-effect)補償。
而在低頻時,C3等於開路,增益極高,在較高頻率時,C3的電抗減少,並開始變成Q3的負回授迴路。而在高頻時,幾乎所有來自Q1的信號電流都流經C3,而不流經R2和Q3基極。在這種情況下,我們簡直可以把Q3想做是一個運算放大器,而其基極的節點(node)就像實效接地(Virtual ground)般,中到高頻時,在Q3集極處的電壓大約等於來自Q1的信號電流乘以C3的電抗值。我們可以更進一步的導出放大器的開迴路增益就等於差動放大器的互導(gm)(此處大約為10mA/V)乘上C3的電抗。由於電抗值是隨頻率每上升一個八度音程降低6dB,而放大器的開迴路增益也會同樣幅度降低,當此增益降至20時,就是增益交越頻率(fx)了,這是因為由回授路徑所形成的閉迴路增益(Gc)是20,若C3的數值選用84pF,則1MHz時的電抗約為2K歐姆,而使得增益在該頻率處交越,同時產生圖二下層的開迴路增益曲線。表三以一般的形式則是:


注意諸如回授因數的低頻考慮並不影響C3數值的選擇。
傳播遲延
有些論文的作者曾做如此推論:暫態非常快速的放大器在回授信號到達輸入端來抵消大部分的輸入信號前,會有短暫的一段時間失卻負回授,即回授信號遭到遲延。他們竟因而推論出在這段遲延的時間內,開迴路放大器中的某些放大級會在輸入有大得不尋常的信號時產生割切現象。
如果加到這個音頻放大器上的信號是上升時間為1nS的方波,這種問題或許毫無疑問的會發生在評估這種問題的實質可能性時,我們應當考慮實際節目源信號的上升時間為何,真正遲延了時間是多少(而不是某些人所暗示的開回路上升時間),以及開迴路放大器增益級中的過載產生機構為何等。


開迴路放大器可以如圖五所示般,用一個增益單元,一個主要的(dominant)一階(first order)補償滑落,及一個代表純遲延的單元來替代,而其他非主要極點的效果可以總括在遲延單元內。但精確度會稍有損失,此時如果在一階的RC低通濾波器輸入端有一個步級的變化,則輸出立刻開始變化,而不論RC時間常數有多長,只不過其變綠將是此依時間常數而定,這是我們所熟知的。因此放大器的輸入有突然變化後,這就是放大器的傳播遲延(propagation delay)時間,也是真正會讓放大器過載的時間,而為了應付前面所提過的問題,這正是我們所必須注意的一段時間。
傳播遲延時間可經由對回授迴路的相位邊際加以考慮而預估出來,如果放大器在增益交越頻率1MHz時的相位邊際是45°,則順向路徑(forward path)(假設為平直的)的遲延總計必須為135°,其中大約有90°是來自補償的極點,而其餘的45°是來自傳播遲延,這個數字可換算成125nS的時間,而大多數放大器的傳播遲延都比這個數字少得很多。
同時我們在此要指出,說放大器在這段時間內失卻回授是不正確的,只要增益、滑落及遲延單元都能保持線性,這個閉迴路放大器仍將是一個線性的系統,同時也是一個連續的系統,而不論遲延如何。同時只要在任何一級都尚未開始產生割切現象前,回授都會100%的出現,只不過是持續的「趕不上」罷了,期趕不上的差距正好和遲延時間相當,所幸的是,回授方程式早已把這種遲延列入頻域(frequency domain)和時域(time domain)的考慮中了。
然而會不會有一個像頻帶受限的方波般的滿值輸入信號,其上升時間能高達125nS,而導致任一放大級呈現非線性或過載呢?答案是補償單元的積分作用會使其後的各級免於過載,獨留下在此以前的輸入級有此憂慮(見圖四)。
試想一個最糟的情形,輸入為一個峯值2V、頻帶受限於20KHz的方波,在125nS內會上升到63mV,這已經足以使輸入級呈現非線性了,這在沒有射極電阻的差動晶體對尤為正確(此一局部回授通常稱作射極衰減。如圖四的設計所示,誤差信號輸入後,小信號增益降至標稱值的一半以下,這種情形時的非線性會導致「軟性」(soft)的TIM。然而,大多數的高級放大器設計都有某種充分的局部回授,讓輸入級能有良好的線性來處理這種誤差信號,稍後我們看到這種回授也是達成高折轉率的重要因素。
此處,回授因數和開回路頻寬之間很明顯是不相關的,這是由於許多參數值不同的設計,也會有相同的輸入級設計及傳播遲延,在此的重要準則是讓輸入級能線性的處理大輸入信號,至少要在暫態情況下能如此。
轉載音響技術第54期JUN. 1980 不談線性IC/第一部分──以另一角度來剖析TIM/Robert R. Cordell 著/蘇天豪 譯/


 留言列表
留言列表


